The two-sample test app is a common fixture of intro stats, deservedly or not. It’s usually described as addressing this question: Is there a difference in the means of two groups? A nice example in the OpenIntro stats book1 looks at the difference in birth weight of babies born to smokers and non-smokers. They give the following summary statistics, where the units of the mean and standard deviations are in pounds and n is the number of babies in each group.
| smoker | nonsmoker | |
|---|---|---|
| mean | 6.78 | 7.18 |
| sd | 1.43 | 1.60 |
| n | 50 | 100 |
You could forgive a student who thinks that the table above gives the “data” for the problem. Indeed, this is the only input needed for all the usual formulas involved in the two-sample t-test. The OpenIntro project gives more context, providing the full 150 cases and several variables:2
The Little App on the two-sample t-test3 has two distinct goals:
- Put the t-statistic in the context of the actual data, so that students can see that the mean is not the only message.
- Provide a basis for students to visualize the t-test that puts it in a less abstract domain than implied by the textbook formulas.
There’s also a third goal that’s oriented toward instructors:
- Help instructors see that the t apparatus provides only a small refinement on what can be seen more straightforwardly by comparing confidence intervals for the two groups. Personally, I think the t-test ought to be taught as a specialized, technical method for dealing with a particular situation, that of having very small sample sizes (say, n < 10).
Finally, remember that there are interesting stories that can be revealed by the NHANES data. Make sure to relate the data display and statistical annotations to those stories and to ask students to translate them into everyday terms. And, in those situations where the interesting part of the story is not about the mean, but about some other aspect of the distribution, be sure to point that out.
Orientation to the app
Like many other Little Apps, the two-sample t-test app centers on a data display with a response variable on the y-axis and the explanatory variable on the x-axis. In this setting, the explanatory variable is always categorical with two levels, but the response variable can be any quantity. Given that the explanatory variable is categorical, a jittered scatter plot is used to display the data. The statistics provide an annotation on the data.
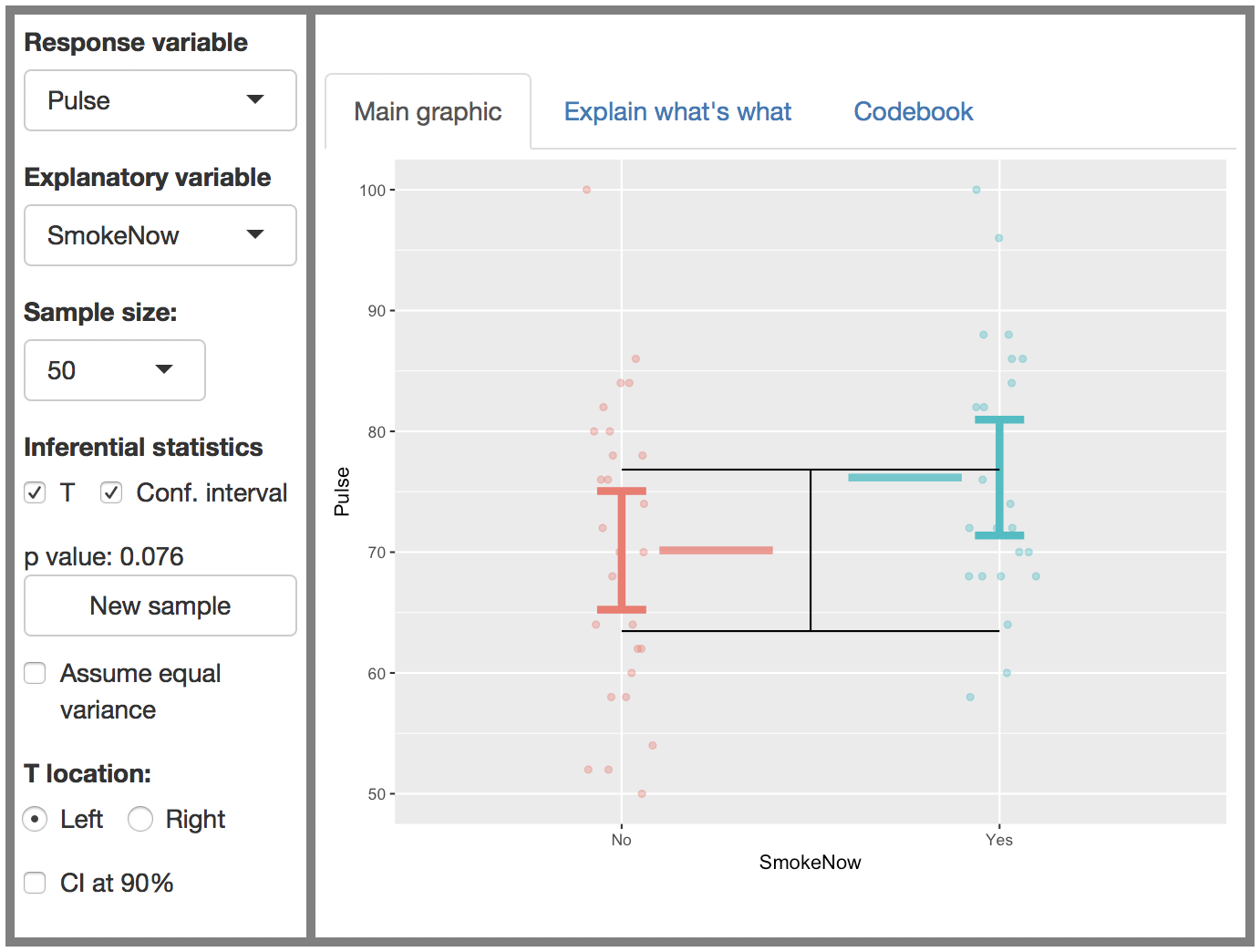
Also like other Little Apps, this one makes use of the National Health and Nutrition Evaluation Survey data in the NHANES data table. There are controls to select the response and explanatory variables and the size of the sample (which will be drawn from the 10,000 cases in NHANES).
We’ll talk about the other controls (e.g. the button to collect a new sample) as they are needed.
Teaching with the app
There are other Little Apps that are better suited for introducing confidence intervals, so this two-sample t-test app is intended for use after students already understand the idea of a confidence interval. What this app adds is the t-test mechanism for comparing two confidence intervals to one another.
I’d suggest using this app for different lessons on two different days. The first lesson is about looking for overlap between two confidence intervals: what this looks like, what this means, etc. The second lesson introduces t, a more formal way to summarize what can be judged from the overlap of confidence intervals. A third lesson reveals the potential problem introduced by searching for variables that produce a positive result. I’ll be interested to find out whether instructors come to conclude that t is no big deal and wonder why it’s so central to the traditional introductory curriculum. If you reach this conclusion, rest assured that statistics is still a big deal. By deprioritizing the t-test in the curriculum, we’ll leave time for statistical methods such as regression that enable us to reveal and quantify interesting and important patterns in data.
Overlapping confidence intervals
Start with an example such as age-at-first-baby vs working status, smoking status, or home ownership. Set the sample size at n=500 and leave off the confidence interval and t annotations. Have students interpret the difference between the means in everyday terms.
Then move the question to whether this result is reliable. One way to find out is to collect many samples and see if we get a similar result in most of them. Pressing the new-sample button many times, you’ll see that the means tend to stay in small, non-overlapping regions. Now change the sample size to n=50. As you collect new samples, the means will jump around much more: there isn’t enough data in each sample to make a precise enough estimate of the mean to get reliable results. (It might be that just one sample trial in 10 produces means that are inverted from the usual pattern. There’s a nice discussion to be had here about what should be the threshold on the frequency of such inversions to define a “reliable” result. No more than one in twenty? One in fourty? One in one hundred?)
Time to point out that in the real world it’s hard to collect a new sample. So we need to judge from the one sample at hand what might have happened if we collected a new sample. This is the role of confidence intervals.
Turn on the confidence interval annotation. Revisit examples you used previously. The confidence interval is based on just the data in the sample being displayed. A good way to decide whether a difference in means is reliable is to check whether the two confidence intervals overlap. You may be asked, “How much overlap is allowed?” A good answer is to say that, for the present, we’ll insist that reliability means no overlap at all. But later we’ll see a way to be more subtle about this.
Display an example where the confidence intervals do not overlap. Don’t hunt4 for one by taking many trials with the same n, explanatory variable, and response variable. The emphasis should be that real work is done with the sample at hand, not by fishing for the lucky sample that happens to show what you want. You might want to fix on the example before class, so you can just bring up that example without hunting.
Once you’ve established that the confidence intervals do not overlap, turn off the display of confidence intervals. How look at many new samples of the same size and see how often, if at all, the difference between the means is inverted in that sample. Or, if your students have access to the app, have them set the explanatory and response variables and n to match yours, and generate many new samples, keeping track of the number of trials in which inversion does or does not occur. Collate and display the results to the class. Point out what ought to be amazing: by doing a confidence interval calculation on one sample, you’re able to predict pretty well what will be seen in the many other samples that were subsequently taken. This is the sense in which confidence intervals can tell you about the reliability of a result.
Repeat the exercise but with a small n where there is considerable overlap (say by 1/4) of the two confidence intervals. Now the frequency of inversion will be much greater.
Finally, ask student to choose arbitrarily a response and explanatory variable. Use n=100 or so. Bring up one sample, displaying confidence intervals. Do they overlap? Then, turning off the confidence intervals, draw many new samples and tally the fraction where the difference in means is inverted. Formally, this is the same as you’ve already done, but it will seem like less of a trick if the students get to define the variables.
Show that, given the variables, the length of the confidence intervals depends on n.
Using t
It’s another day in class. Take a few minutes to review the previous lesson: that the overlap or non-overlap of confidence intervals allows you to make a pretty good prediction of how often a new sample trial will give an inverted difference in means.
Remind them that there is a question: How much overlap can be allowed before concluding that the difference in means cannot be known reliably from the sample at hand? Statisticians have adopted another more formal approach which avoids the issue. Instead of calculating the confidence intervals of the two means and comparing, calculate just one confidence interval on the difference between the means. Turn on the t interval display.
The black sideways-H interval on the screen shows this confidence interval on the difference between means. One of the two means will always be in the center of the interval. That’s because the interval itself is centered on the actually observed difference in sample means. It’s the length of the interval that brings in the information about the separate confidence intervals on each mean.
Typically, one of the means will not be in the center of the interval. Let’s call this group A. The question of reliability of the difference between means comes down to whether the mean of group A falls inside or outside of the black sideways-H interval. By turning on the display of the confidence interval of the individual means, you can show that group A being outside the sideways-H interval means that there is little or no overlap between the confidence intervals on the individual means.
Variation in t
Still another day in class. Pick a response and explanatory variable of interest (or ask your students to pick). Show the t-interval and the intervals on the individual means. Now run new sample trials and observe that the t-interval is itself somewhat random.
This trial-to-trial variation in t creates a problem of potential importance in interpreting results from statistical studies.
The t-interval calculation is based on several assumptions, one of which it this:
Valid t calculation: The sample was collected with pre-determined n for the purpose of examining the relationship between a pre-determined response variable and a pre-determined explanatory variable.
But something different often happens:
Invalid t calculation I: You have a dataset with many variables. You search for some response and explanatory variable that produces a t-interval indicating a reliable difference between group means. Then you publish a report about those two variables without describing all the other comparisons you made with other variables that didn’t not turn out to give a positive result.
This is called the problem of multiple comparisons.
There’s also a version of the problem which involves a community effect where many studies are being performed, each individual one of which is done in a way that produces a valid t calculation.
Invalid t calculation II: There are several (or many) different studies being done about the possible relationship between an explanatory and a response variable. Perhaps almost all of the studies fail to find a positive result. But the person who happened to get a positive result – remember, t varies from sample to sample – publishes their result while the others don’t. Possibly the successful person didn’t even know about the other studies. Or perhaps they knew about some of them but they think that they are a better scientist and did the study properly while the others did not.
In order properly to interpret a study, you need to know about the context in which the study was performed. Studies where the outcome and explanatory variable(s) are specified before data collection should be taken more seriously than studies that didn’t do this. You can be more comfortable with the results of a study which follow up on some previous hypothesis with new data. And for a result to be taken as definitive, the sample size n should be large enough that the confidence intervals are far from overlapping.
Often this non-overlapping is described in terms of a p-value. The sample size n should be large enough that p is very small. And forget about 0.05 or 0.01 as being very small. Those values were suggested (by Ronald Fisher in the 1930s) for the purposes of screening preliminary results to get an idea of which ones are worth follow-up studies. Once a hypothesized relationship has passed the screening test, it’s time to collect new data and much more of it.
As an instructor, you should take this notion of screening seriously. Screening tests are intended to be relatively easy and cheap, and then be followed up with more definitive testing. The standard of evidence provided by a p near 0.05 is very low. One place this is forgotten is the misplaced topic of one- vs two-tailed tests. If you got p < 0.05 by using a one-tailed rather than a two-tailed test, the situation is still that p is near 0.05 and not, say, near 0.0001. Just stick with the two-tailed test. And remember that the 0.05 threshold dates from a time when there were relatively few statistical research projects and publications, not the huge number that we see today.
For instructors
There are two controls in the two-sample t-test app that are intended for instructors. The first is the checkbox “use equal variance.” Some textbooks continue to take up time and space introducing the unequal variance t-test. This version of the t-test is of no practical importance. By checking and unchecking the equal-variance box, you can get an idea of how much it changes (or doesn’t change) the overall result. Keep in mind that any small changes in p that result from using one test or the other should be put in the context of the variation in t described in the previous section.
The second control for instructors is the “CI at 90%” checkbox. This simple modification to the level at which the confidence intervals are calculated provides a pretty good practical answer to the “how much overlap” question. Non-overlap of the CIs at a 90% confidence interval gives a result close to that of the t-test at 95%.
OpenIntro Statistics, 3rd edition, section 5.3.2, see openintro.org.↩
See the
birthsdata frame (in theopenintropackage).↩Framing this problem as a t-test is a statistical dead end. There are many potential covariates here. If one’s goal is to understand how smoking contributes to the outcome, one should use a method that is more flexible, for instance regression methods. And why is it that we’re interested in the mean baby weight? Might it be more medically meaningful to look at the probability of a baby being underweight?↩
Sometimes called“data peaking”, or “p-hacking”. The term “data mining” is also used to describe such hunting. This usage is mostly unrelated to a contemporary set of machine learning techniques described by the same name that mine data for genuine relationships in the same way that one mines for gold in a mass of otherwise worthless rock.↩
